«Определение вероятности попадания в цель на основе метода Монте-Карло (при стрельбе ракетами)» 1. Разработка Генератора случайных чисел (ГСЧ), имеющих равномерное распределение на интервале [0,1] (Использование стандартной функции).
- Теория вероятностей
Условие:
Выполнить лабораторную работу:
«Определение вероятности попадания в цель на основе метода Монте-Карло (при стрельбе ракетами)»
1. Разработка Генератора случайных чисел (ГСЧ), имеющих равномерное распределение на интервале [0,1] (Использование стандартной функции).
2. Получение N случайных чисел и их использование для расчета количества попаданий в цель на основе метода Монте-Карло.
3. Расчет вероятности попадания в цель.
Выводы о возможности использования метода Монте-Карло для расчета вероятности попадания в цель.
Бомбардировщик атакует промышленное предприятие как показано на рис. 1 ракетами класса «воздух – земля». Каждая ракета наводится индивидуально. Размеры предприятия М - длина и Н – ширина метров. Заход на атаку производится с направления, совпадающего с направлением длинной оси цели.
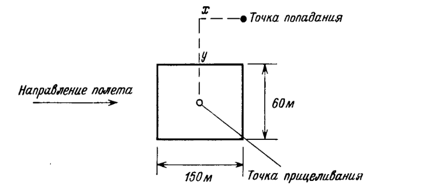
Рис. 1 Направление атаки бомбардировщика
Точка прицеливания – геометрический центр цели. Фактическую точку попадания каждой ракеты можно определить горизонтальным отклонением Х и вертикальным отклонением Y. Для расстояния, с которого запускаются ракеты, оба распределения независимы, имеют нормальное вид относительно точки прицеливания и нулевое среднее значение. Среднеквадратическое отклонение в направлении х имеет значение К, а в направлении Y – значение Р. Бомбардировщик при каждом заходе выпускает В ракет.
Оценить среднее число попаданий при каждой атаке, взяв объем выборки в П заходов.
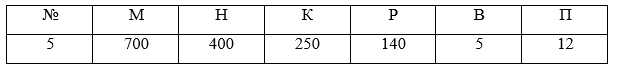
Решение:
Ход работы
Для получения пары значений стандартной нормально распределенной случайной величины воспользуемся методом Бокса и Маллера:
1. Используем два случайных равномерно распределенных числа r1, r2.
2. Полагаем 1=-1+2r1, 2=-1+2r2 и вычисляем S=12+22.
3. Если S1, возвращаемся на шаг 1, иначе:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства