Условие задачи
Вероятность выиграть у равносильного противника равна
p = 0,5,
Соответственно вероятность проиграть у равносильного противника равна
q = 1 – p = 1 – 0,5 = 0,5
Найдем и сравним такие вероятность Р5(3) и Р8(5)
Поскольку количество испытаний невелико (n = 5 и n = 8), то для нахождения вероятности того, что событие А появится точно k = 3 раза (k = 8 раз) воспользуемся формулой Бернулли:
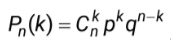
где q = 1 – p
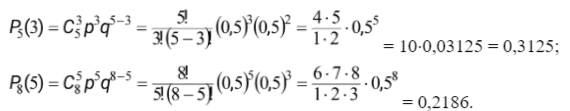
Сравнивая полученные значения вероятностей Р5(3) = 0,3125 > Р8(5) = 0,2186 получаем, что вероятнее выиграть у равносильного противника три партии из пяти чем пять из восьми.
Ответ
Вероятность выиграть у равносильного противника равна:
p = 0,5,
Соответственно вероятность проиграть у равносильного противника равна:
q = 1 p = 1 0,5 = 0,5
Найдем и сравним такие вероятность Р5(3) и Р8(5)
Поскольку количество испытаний невелико (n = 5 и n = 8), то для нахождения вероятности...
