Условие:
С целью определения средней величины транспортных затрат (тыс.руб.) на доставку одной тонны продукции предприятий пищевой промышленности к потребителям в некотором крупном мегаполисе, имеющем 2570 предприятий, по схеме собственно-случайной бесповторной выборки проведено обследование 240 предприятий. Распределение транспортных затрат (тыс. руб.) представлено в таблице:
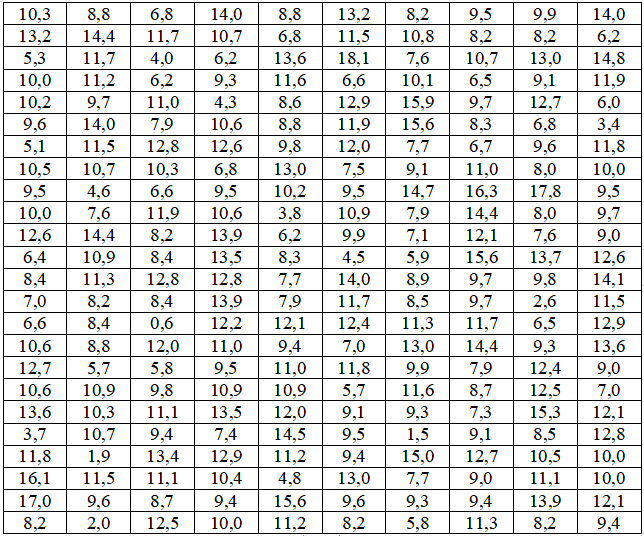
1. Составить интервальный вариационный ряд. Построить гистограмму и полигон частот (на одном графике), эмпирическую функцию распределения (кумуляту).
2. По сгруппированным данным вычислить выборочные числовые характеристики: среднее арифметическое, исправленную выборочную дисперсию, среднее квадратичное отклонение, коэффициент вариации, асимметрию, эксцесс, моду и медиану.
3. Используя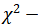 
критерий Пирсона, на уровне значимости проверить гипотезу о том, что случайная величина 
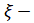величина транспортных затрат (тыс. руб.) на доставку одной тонны продукции – распределена по нормальному закону. Построить на чертеже, содержащем гистограмму эмпирического распределения, соответствующую нормальную кривую.
4. Предположив нормальность распределения транспортных затрат (тыс. руб.) на доставку одной тонны продукции, на 5%-ном уровне значимости проверить следующие гипотезы:
а) о числовом значении математического ожидания, приняв в качестве нулевой гипотезы 
средняя арифметическая, при альтернативной гипотезе ;
б) о числовом значении дисперсии, приняв в качестве нулевой гипотезы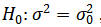 
, где в качестве 
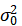взять исправленную выборочную дисперсию при альтернативной гипотезе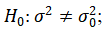 
в) о числовом значении вероятности события, состоящего в том, что величины транспортных затрат (тыс. руб.) на доставку одной тонны продукции составляет в пределах от 12 до 17 тыс. руб., приняв в качестве нулевой гипотезы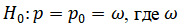 
- соответствующая выборочная доля, вычисленная по не сгруппированным данным, при альтернативной гипотезе 
5. Предположив нормальность распределения величины транспортных затрат (тыс. руб.) на доставку одной тонны продукции, требуется:
а) построить 95%-ные интервальные оценки математического ожидания, дисперсии, среднего квадратичного отклонения и вероятности события, рассмотренного в п. 4в;
б) определить вероятности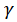 
того, что генеральная средняя, генеральное среднее квадратическое отклонение и генеральная доля, рассмотренная в п. 4в, отличаются от соответствующих им выборочных характеристик не более чем на 5%, т.е. оцениваемый параметр генеральной совокупности t накрывается интервалом 
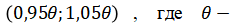соответствующая выборочная оценка;
в) определить объемы выборок, чтобы те же границы для генеральной средней и генеральной доли (п. 5б), гарантировать с вероятностями, большими, чем полученные в п. 5б, на 50% от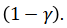 
Решение:
1. Находим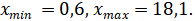 
Размах выборочных значений:
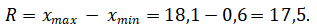
Объём выборки