Система S может находиться в двух состояниях. В начальный момент времени система находится во втором состоянии. В системе протекает марковский процесс с непрерывным временем

23 января 2025
Теория вероятностей

Условие:

Система S может находиться в 2-х состояниях. В начальный момент времени система находится во 2-м состоянии. В системе протекает марковский процесс с непрерывным временем, интенсивности простейших потоков, переводящих систему из состояния в состояние, указаны на размеченном графе:

Записать систему дифференциальных уравнений Колмогорова, найти вероятности состояний, решив систему операционным методом. Найти предельные вероятности состояний предельным переходом.

Решение:

Систему дифференциальных уравнений Колмогорова записываем по размеченному графу состояний (производная вероятности состояния равняется сумме входящих поток вероятностей за вычетом исходящих потоков):

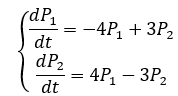
Найдем решение полученной системы уравнений операционным методом. Применяем преобразование Лапласа (т.к. начальный момент времени система находится во 2-м состоянии, то P₁ (0)=0,P₂ (0)=1):