1. Главная
  2. Библиотека
  3. Сопротивление материалов
  4. Стальная рама (модуль упругости E=2·105 МПа) нагружена сосредоточенными силами P, парой сил M и равномерно распределенными...

Стальная рама (модуль упругости E=2·105 МПа) нагружена сосредоточенными силами P, парой сил M и равномерно распределенными силами интенсивностью q. Схемы нагружения рамы представлены на рис.

«Стальная рама (модуль упругости E=2·105 МПа) нагружена сосредоточенными силами P, парой сил M и равномерно распределенными силами интенсивностью q. Схемы нагружения рамы представлены на рис.»
  • Сопротивление материалов

Условие:

Стальная рама (модуль упругости E=2·105 МПа) нагружена сосредоточенными силами P, парой сил M  и равномерно распределенными силами интенсивностью q. Схемы нагружения рамы представлены на рис.  

Требуется: 

1. Определить внутренние силовые факторы (продольные силы N, поперечные силы Qy и изгибающие моменты Мz) в поперечных сечениях рамы, построить их  эпюры. 

2. Из условия прочности по нормальным напряжениям подобрать двутавровое сечение, приняв значение допускаемых напряжений [σ]=160МПа. 

3. Определить горизонтальное, вертикальное и полное перемещение заданного сечения рамы. Определить направление полного перемещения заданного сечения. Исходные данные, определяющие силу Р, момент пары сил М, интенсивность распределенной нагрузки q, длину a, представлены  в таблице  2.  

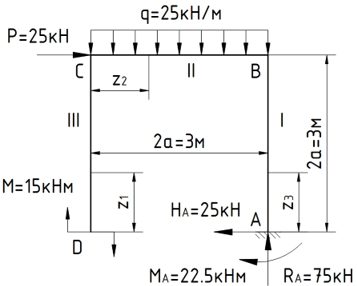
Дано:

Р=25 кН

М=15 кНм

q=25 кН/м

а=1.5 м

Решение:

1. Определим реакции в заделке

Fx=0

PHA=0

HA=P=25 кН

Fy=0

RAq2a=0

RA=q2a=253=75 кН

МA=0

MA+q2aaP2aM=0

MA=q2aaP2aM=2531.525315=22.5 кНм

Проверка:

МС=0

Mq2aaHA2aMA+RA2a=0

152531.525322.5+753=0

0=0

2. Определяем значения изгибающих моментов, поперечных и продольных сил в поперечных сечениях плоской рамы.

0 z1 3м

Mx(z1)=M=15 кНм

Qy(z1)=0

Nz(z1)=0

0 z2 3м

Mx(z2)=Mqz2z2/2

Mx(0)=15 кНм

Mx(3)=152531.5= 97.5 кНм

Qy(z2)= qz2

Qy(0)=0

Qy(3)= 253= 75 кН

Nz(z2)= Р= 25 кН

0 z3 3м

Mx(z3)= MAHAz3

Mx(0)= 22.5 кНм

Mx(3)= 22.5253= 97.5 кНм

Qy(z3)= HA=25 кН

Nz(z3)= RA= 75 кН

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я