1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. Вероятность попадания в цель при одном выстреле равна  p =0,6. Выстрелы производятся в независимости друг от друга. С.в. X...

Вероятность попадания в цель при одном выстреле равна  p =0,6. Выстрелы производятся в независимости друг от друга. С.в. X показывает число попаданий при n =4 выстрелов. С.в. Y показывает число попаданий из m=300  выстрелов.

«Вероятность попадания в цель при одном выстреле равна  p =0,6. Выстрелы производятся в независимости друг от друга. С.в. X показывает число попаданий при n =4 выстрелов. С.в. Y показывает число попаданий из m=300  выстрелов.»
  • Теория вероятностей

Условие:

Вероятность попадания в цель при одном выстреле равна  p =0,6. Выстрелы производятся в независимости друг от друга. С.в. X показывает число попаданий при n =4 выстрелов. С.в. Y показывает число попаданий из m=300  выстрелов.

1. Найти математическое ожидание, дисперсию, моду с.в. Х

2. Найти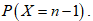

Найти вероятности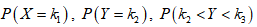  

Решение:

1. Случайная величина подчинена закону распределения Бернулли.

Математическое ожидание М(Х)=np=4*0,6=2,4

Дисперсия D(X)=npq=4*0,6*0,4=0,96

Мода биномиального распределения определяется выражением

Mo = trunc[(n +1)p], где функция trunc[(n +1) p ] обозначает целую часть числа (n +1)p .

Если число (n +1)p целое, то распределение имеет два модальных значения (n +1)p и (n +1) p -1.

(n+1)p=5*0,6=3 целое

Мода Мо=2 и 3.

2. Случайная величина X имеет область значений (0,1,2,...,n). Вероятности этих значений можно найти по формуле

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я