1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. Ниже приведены 50 значений случайной величины X, а также вычисленные по выборке среднее a и среднее квадратическое s....

Ниже приведены 50 значений случайной величины X, а также вычисленные по выборке среднее a и среднее квадратическое s. Используя критерий хи-квадрат, определить, будет ли X нормальной случайной величиной.

«Ниже приведены 50 значений случайной величины X, а также вычисленные по выборке среднее a и среднее квадратическое s. Используя критерий хи-квадрат, определить, будет ли X нормальной случайной величиной.»
  • Теория вероятностей

Условие:

Ниже приведены 50  значений случайной величины X, а также вычисленные по выборке  среднее  a  и среднее квадратическое s. Используя критерий хи-квадрат, определить, будет ли X нормальной случайной величиной. В  качестве  уровня  значимости взять вероятность 0,2.

75,80 87,62 80,93 75,94 84,80 80,19 91,43 78,64 81,02 70,35

67,86 75,48 74,99 85,23 78,68 88,48 64,75 74,14 90,65 96,54

77,95 84,15 64,21 75,51 82,06 65,40 76,34 85,67 81,10 81,49

72,97 68,22 80,63 70,01 86,28 86,80 80,04 67,90 81,56 79,34

92,18 86,29 70,11 74,67 71,10 72,39 70,43 78,57 85,75 77,60

a = 78,60     s =  7,636

Решение:

Объем выборки n = 50.

Минимальное значение хmin = 64,21; максимальное значение хmах = 96,54;

размах: 96,54 64,21 = 32,33.

Проведем группировку исходных данных. Количество интервалов подсчитаем по формуле Стерджесса: k = 1+3,322∙lg n k = 1+3,322∙lg 50 7.

Так как вычисленное количество интервалов 7, то выборку разобьем на 7 равных интервалов. Величина отдельного интервала:

.

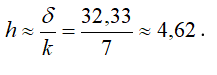Получим интервалы:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я