Условие:
Для варианта системы в пространстве состояний рассчитать матричную экспоненту, а затем рассчитать в MatLab значение матричной экспоненты в различные моменты времени.
Построить матричную передаточную функцию. Проверить полученное описание моделированием в MatLab.
Исходные данные
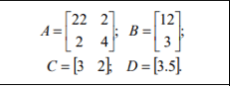
Краткие теоретические сведения
Свободное движение системы в пространстве состояний описывается формулой:
X(t) = Ф(t)X(0).
где X(0) – начальное состояние системы; X(t) –состояние системы в момент времени t, Ф(t) – матричная экспонента:
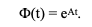
Матричная экспонента также называется фундаментальной матрицей или переходной матрицей состояния
Решение:
Ход работы
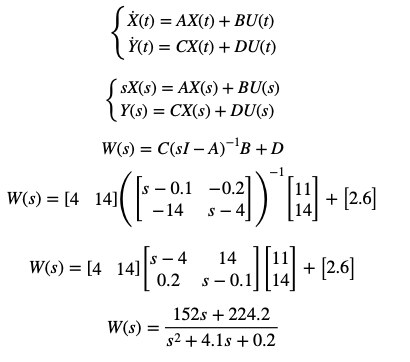
Моделирование в Simulink:
