Условие:
Исходные данные
Задан объект управления в виде дифференциального уравнения
где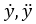 
– первая и вторая производные от выходной переменной ;
u – управляющее воздействие.
Функция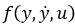 
для заданного варианта представлена в табл.1.1.
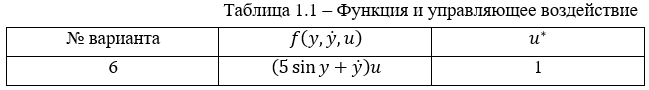
Требуется выполнить:
1) представить дифференциальное уравнение (1.1) в пространстве состояний (в фазовом пространстве);
2) найти дифференциальное уравнение для фазовых траекторий по второму методу;
3) найти особые точки фазовых траекторий системы по п.1 при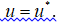 
.
Решение:
1. Вводим обозначения:
где x1, x2 переменные состояния.
Тогда исходное дифференциальное уравнение
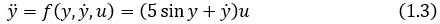
в пространстве состояний (в фазовом пространстве) преобразуется в систему уравнений:
