Условие задачи
Объект управления – вертолет, движущийся в вертикальной плоскости. Управление движением осуществляется с помощью наклона плоскости несущего винта на угол σ.
Динамические параметры движения: ϴ – угол тангажа, x – перемещение в горизонтальном направлении. В качестве математической модели процесса стабилизации рассматривается СЛДУ:
Где a1=-0.415, a2=-0.0111, b1=6.27, a3=9.80, a4=-1.43, a5=-0.0198, b2=9.80. При этом ϴ измеряется в радианах, а x – в метрах.
Задача системы стабилизации – удержать машину в заданном положении при воздействии внешних возмущений.
Содержание работы:
1. Сформировать LTI-объект, соответствующий данной модели. Входом считать переменную σ , а выходом – вектор y с компонентами ϴ и x .
2. Найти передаточные функции от входа к выходным переменным. Построить диаграммы Боде для этих функций в диапазоне частот ω={0.1…1000}.
3. Определить нули и полюса передаточных функций.
4. Создать frd-объект для частотного анализа модели. Проверить, что объект соответствует созданному в п. 2
Ответ
Динамические свойства объекта регулирования и элементов САР описываются следующей системой уравнений:
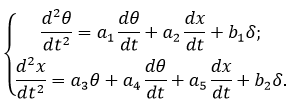
За переменные состояния примем выходы системы и их производные:
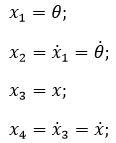
Тогда исходную систему уравнений мож...
