По заданной системе дифференциальных уравнений, описывающих работу системы автоматического управления (САУ) необходимо: 1. Составить структурную схему САУ. 2. Найти передаточную функцию разомкнутой системы используя правила структурных преобразований. 3.
- Автоматика и управление
Условие:
По заданной системе дифференциальных уравнений, описывающих работу системы автоматического управления (САУ) необходимо:
1. Составить структурную схему САУ.
2. Найти передаточную функцию разомкнутой системы 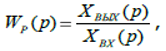 используя правила структурных преобразований.
используя правила структурных преобразований.
3. Построитьасимптотическую логарифмическую амплитудно-частотную (ЛАЧХ) и логарифмическую фазо-частотную характеристики (ЛФЧХ) и амплитудно-фазовую частотную характеристику (АФХ) разомкнутой САУ.
4. Проверить правильность выполнения п.3, построив ЛАЧХ, ЛФЧХ и АФХ с помощью макета прикладных программ MathCAD.
5. Найти передаточную функцию замкнутой САУ и оценить ее устойчивость с помощью критериев Найквиста и Гурвица, а также с помощью необходимого и достаточного условия устойчивости, найти предельный коэффициент усиления.
6. Построить временные характеристики (переходную и весовую) замкнутой системы.
7. Смоделировать замкнутую систему в Simulink Matlab и построить переходную и весовую функцию системы; сравнить полученные характеристики с характеристиками, полученными в п.6.
8. Определить установившиеся значения сигнала 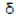 при подаче на вход САУ воздействий в виде единичного скачка
при подаче на вход САУ воздействий в виде единичного скачка 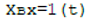 и линейно возрастающего сигнала
и линейно возрастающего сигнала 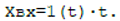 Сравнить определенные значения со значениями, полученными по модели системы в Simulink Matlab.
Сравнить определенные значения со значениями, полученными по модели системы в Simulink Matlab.
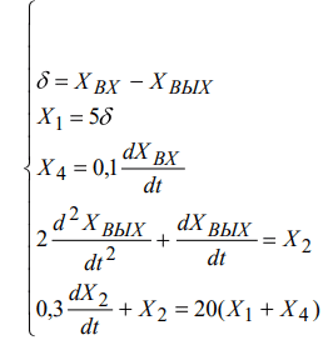
Решение:
1. Зная диф. уравнения объектов, запишем уравнения в операторной форме:
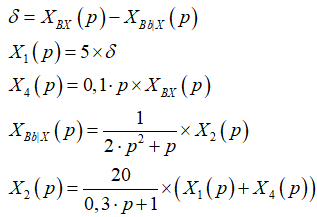
На основании системы уравнений формируем структурную схему:

2.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства