Очень длинный цилиндр из диэлектрика (относительная диэлектрическая проницаемость ε = 4,0), радиус которого R = 5,0 см, заряжен с объёмной плотностью ρ = ρ0∙r/R, где r – расстояние от оси цилиндра, а ρ0 = 3,0∙10–6 Кл/м3.
- Физика
Условие:
Очень длинный цилиндр из диэлектрика (относительная диэлектрическая проницаемость ε = 4,0), радиус которого R = 5,0 см, заряжен с объёмной плотностью ρ = ρ0∙r/R, где r – расстояние от оси цилиндра, а ρ0 = 3,0∙10–6 Кл/м3. Найти зависимости электрического смещения, напряжённости и потенциала электрического поля от расстояния от оси цилиндра (принять потенциал равным нулю на оси цилиндра) и построить соответствующие графики.
Вычислить: заряд, приходящийся на единицу длины цилиндра; энергию поля внутри цилиндра, приходящуюся на единицу его длины; потенциал на поверхности цилиндра и на расстоянии r1 = 10 см от его оси. Построить графики зависимостей объёмной плотности свободных и связанных зарядов от расстояния от оси цилиндра.
Решение:
Согласно теореме Гаусса, поток электрического поля через поверхность соосного с данным цилиндра равен:
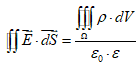 . Применим данную теорему для соосного с заданным цилиндра данную теорему, поскольку в нашей задаче цилиндрическое симметричное распределение заряда (плотность зависит лишь от r), то принимая rR для соосного цилиндра получим, что E зависит лишь от r.
. Применим данную теорему для соосного с заданным цилиндра данную теорему, поскольку в нашей задаче цилиндрическое симметричное распределение заряда (плотность зависит лишь от r), то принимая rR для соосного цилиндра получим, что E зависит лишь от r.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства