Привести уравнение кривой второго порядка к каноническому виду. Для эллипса найти координаты вершин и фокусов, для гиперболы – координаты вершин, фокусов и уравнения асимптот, для параболы – координаты фокуса и
«Привести уравнение кривой второго порядка к каноническому виду. Для эллипса найти координаты вершин и фокусов, для гиперболы – координаты вершин, фокусов и уравнения асимптот, для параболы – координаты фокуса и»
- Геометрия
Условие:
Привести уравнение кривой второго порядка к каноническому виду. Для эллипса найти координаты вершин и фокусов, для гиперболы – координаты вершин, фокусов и уравнения асимптот, для параболы – координаты фокуса и уравнение директрисы, для окружности – координаты центра и радиус. Сделать чертеж.
Решение:
Преобразуем исходное равенство:
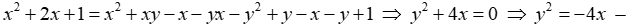
уравнение параболы с вершиной в точке начала координат, ось симметрии проходит через ось Oy, ветви направлены влево.
Координаты фокуса и уравнение директрисы.
Каноническое уравнение параболы: откуда , следовательно, фокус находится в точке
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э