Условие задачи
Дано уравнение sin x + 0.2x – 2 = 0. Отделить корни в интервале [–5, 0] и уточнить один из них заданным методом. Разработать блок-схему алгоритма используемого метода. Результаты представить в виде таблиц (i - хi - f(xi)), и графиков в координатах хi - f(xi), где i - номер шага (итерации).
Отделение корней произвести только графическим методом.
Уточнение корней произвести одним методом (методом деления отрезка пополам).
Ответ
1. Функция f(x) = sin x + 0.2x 2 на отрезке [5, 0] не обращается в 0, немного изменим функцию.
Будем искать корни уравнения функции
f(x) = sin x + 0.2x + 0,5 на отрезке [5, 0]
2. Отделим корни графически, для этого построим график функции
f(x) = sin x + 0.2x + 0.5 на интервале [5, 0].
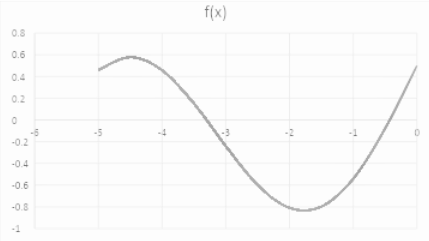
Как видно из графика, ...
Потяни
