Условие задачи
Модуль упругости E=2·105 МПа.
Допускаемое напряжение σadm=160 МПа.
1)Требуется :
вычислить продольные усилия (Ni , кН) и нормальные напряжения (σi , МПа) во всех характерных сечениях стержня, абсолютное (Δli , Δlобщ, мм) и относительное (ε, %) перемещения, величину продольного перемещения (Δln-n, мм) в заданном сечений n-n стержня.
Дано: a= 1.2 м, b=1.4 м, F1=1000 кН, F2=700кН.
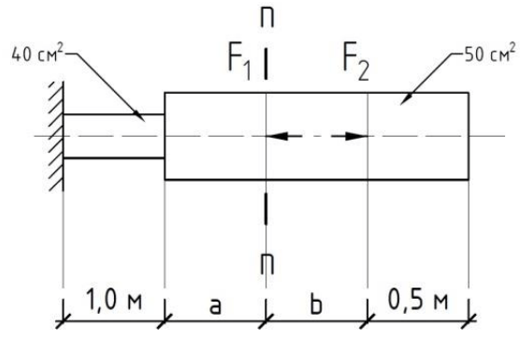
2. Вычертить схему стержня с приложенными силами, соблюдая масштаб размеров по длине стержня и размерам поперечного сечения. Нанести числовые значения размеров и сил на расчетной схеме.
3. Отобразить реакцию опоры и вычислить ее величину; нанести на расчетную схему полученное значение и направление вектора действия реакции.
4. Установить число участков. Под участком понимают часть стержня, в пределах которой не изменяются ни продольная сила, ни площадь поперечного сечения.
5. На каждом участке перпендикулярно продольной оси стержня нанести сечения. Пронумеровать эти сечения арабскими цифрами, например, 1–1, 2–2 и т. д.
6. Для каждого участка вычислить величину продольной силы N1, N2, Ni , …, Nn с учетом знака. Продольная растягивающая сила имеет знак «+», а продольная сжимающая сила – знак «–».
7. Построить эпюру продольных сил N, то есть построить график изменения величины продольного усилия N в сечениях по длине стержня. На эпюре продольных сил следует н указать числовые значения всех характерных ординат, указать символами на графике растянутые и сжатые зоны («+» и «-»).
8. Вычислить величины нормальных напряжений σi для каждого участка σ1, σ2, σi , …, σn по поперечным сечениям. Растягивающие напряжения имеют знак «+», а сжимающие – знак «–».Построить графики нормальных напряжений. На эпюре следует указать числовые значения всех характерных ординат, указать символами на графике растянутые и сжатые зоны («+» и «-»).
9. Вычислить величину продольной деформации для каждого участка Δl1, Δl2, Δli , …, Δln и общую для всего стержня Δlобщ. Деформация удлинения имеет знак «+», а укорочения знак «–».
10. Вычислить продольное перемещение сечения n–n, обозначенного на эскизе задания, Δln-n.
11. Вычислить, на какую величину изменится длина всего стержня, общее продольное перемещение Δlобщ.
12. Вычислить относительную продольную деформацию стержня ε. Примечание. На рис. силы F1 и F2 приложены в точке, соответствующей вершине стрелки.
Ответ
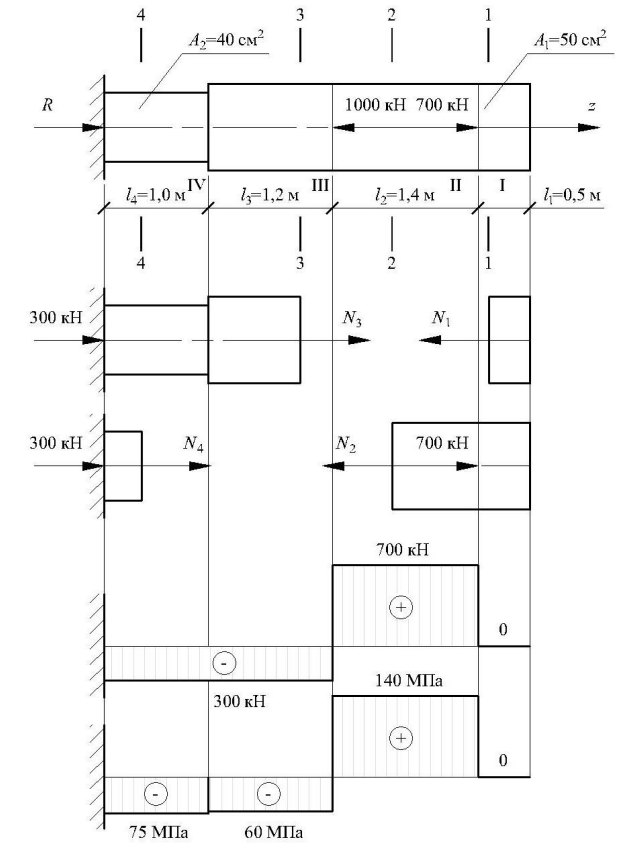
Определение опорных реакций.
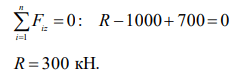
Определение продольных сил на каждом участке.
В данной задаче 4 участка.
Проводим сечение 1-1 и рассмотрим равновесие правой части стержня:
