1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. Аня и Маша независимо друг от друга решают задачу по теории вероятностей. Аня решит её за время X, а Маша - за время Y . В...

Аня и Маша независимо друг от друга решают задачу по теории вероятностей. Аня решит её за время X, а Маша - за время Y . Величины X и Y распределены экспоненциально с параметром 𝜆=3. Обозначим минимальное время решения за L, а максимальное - за R.

«Аня и Маша независимо друг от друга решают задачу по теории вероятностей. Аня решит её за время X, а Маша - за время Y . Величины X и Y распределены экспоненциально с параметром 𝜆=3. Обозначим минимальное время решения за L, а максимальное - за R.»
  • Теория вероятностей

Условие:

Аня и Маша независимо друг от друга решают задачу по теории вероятностей. Аня решит её за время X, а Маша - за время Y . Величины X и Y распределены экспоненциально с параметром 𝜆=3. Обозначим минимальное время решения за L, а максимальное - за R.

(a) Найдите совместную функцию плотности 𝑓𝐿,𝑅(𝑥,𝑦).

(б) Найдите условную функцию плотности 𝑓𝐿/𝑅(𝑥/𝑦).

(в) Найдите условное ожидание E(R / L) и условную дисперсию D(R / L).

Решение:

(а) Найдем совместную функцию плотности 𝑓𝐿,𝑅(𝑥,𝑦) для случайных величин 𝐿=𝑚𝑖𝑛{𝑋,𝑌},𝑅=𝑚𝑎𝑥{𝑋,𝑌}.

Для этого построим совместную функцию распределения 𝐹𝐿,𝑅(𝑥,𝑦)(𝑥𝑦). Применяя определение совместной функции распределения и формулу включения-исключения, запишем (учитываем, что 𝑥𝑦)

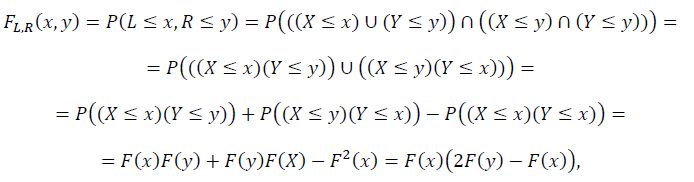
здесь функция распределения экспоненциального закона с параметром 𝜆 (одинаковая для 𝑋 и 𝑌).

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я