Дискретные случайные величины Х1и Х2 имеют биномиальное и пуассоновское распределение соответственно. Известны математические ожидания каждой из величин: МХ1=МХ2=а, и дисперсия величины Х1: D(Х1)=b.
«Дискретные случайные величины Х1и Х2 имеют биномиальное и пуассоновское распределение соответственно. Известны математические ожидания каждой из величин: МХ1=МХ2=а, и дисперсия величины Х1: D(Х1)=b.»
- Теория вероятностей
Условие:
Дискретные случайные величины Х1и Х2 имеют биномиальное и пуассоновское распределение соответственно. Известны математические ожидания каждой из величин: МХ1=МХ2=а, и дисперсия величины Х1: D(Х1)=b. Найти для каждой из величин вероятность того, что случайная величина примет значение, принадлежащее отрезку 
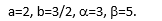
Решение:
Для биномиального распределения 𝑋1
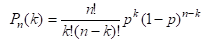
справедливы формулы:
Математическое ожидание 𝑀𝑋1 равно:
𝑀𝑋1=np
Дисперсия 𝐷𝑋1 равна:
D𝑋1=np(1-p)
По условию МХ1=2, DX1=3/2
Тогда np=2, np(1-p)=3/2
Из второго уравнения с учетом первого получим:
1-p=3/4
Тогда р=1/4=0,25
Найдем вероятность событ...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э