Условие:
1. Используя неравенство Чебышева, оценить вероятность того, что случайная величина отклонится от своего математического ожидания 
менее чем на 
, где 
- среднее квадратическое отклонение случайной величины
2. Торговая фирма располагает разветвленной сетью филиалов и есть основания считать, что ее суммарная дневная выручка Х является нормально распределенной случайной величиной. Выявленные значения этой величины по 100 рабочим дням представлены в виде следующего интервального ряда:
Требуется:
1) построить гистограмму относительных частот;
2) определить несмещенные оценки для неизвестных математического ожидания mx и дисперсии Dx= σx2 случайной величины X;
3) найти 95-процентные доверительные интервалы для mx и σx
Исходные данные для решения задач:
Решение:
1. Используем неравенство Чебышева в форме 
, тогда получаем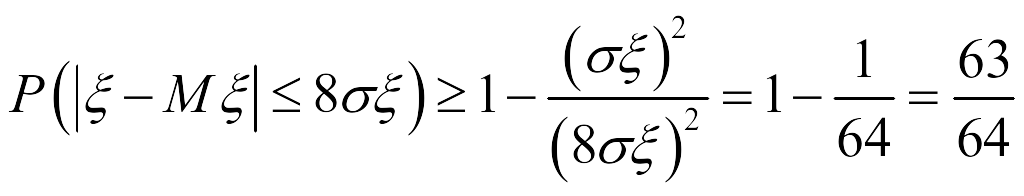 
2. Получаем данные: