"Исследование работы генераторов случайных чисел имеющих заданное распределение" 1. Разработать генератор случайных чисел (ГСЧ) заданного закона распределения на интервале на основе чисел, имеющих равномерное распределение на интервале [0,1]
- Теория вероятностей
Условие:
Выполнить лабораторную работу:
"Исследование работы генераторов случайных чисел имеющих заданное распределение"
1. Разработать генератор случайных чисел (ГСЧ) заданного закона распределения на интервале на основе чисел, имеющих равномерное распределение на интервале [0,1] (Возможно использование стандартной функции).
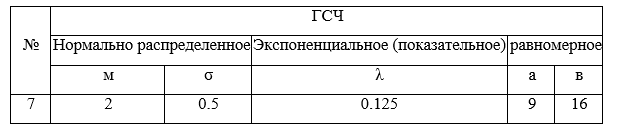
2. Получить N~1000 случайных чисел. Определить границы распределения и частоту попадания чисел в интервалы (количество интервалов 8). Для нормального распределение левая граница распределения равна математическому ожиданию м - 3*среднеквадратических отклонения σ, правая граница равна математическому ожиданию м + 3*среднеквадратических отклонения σ. Для равномерного распределения установить левую границу равной а – правую границу равной в. Для показательного (экспоненциального, Пуассона) распределения: левая граница равна 0 – правая граница равна 5/(интенсивность распределения λ).
3. Сделать выводы о возможности использования ГСЧ для генерации случайных чисел с заданным законом распределения. Была ли принята гипотеза о равномерном распределении
Идентификация полученной выборки с помощью критерия Х – квадрат на соответствие полученного распределения заданному распределению. Необходимо задать границы для входных распределений.
Решение:
Ход работы
1. Приведем формулы для получения соответствующих законов распределения на основе базового равномерного распределения X~R(0;1)
- нормальное распределение с математическим ожиданием и среднеквадратическим отклонением :
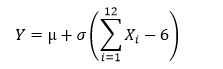
- экспоненциальное распределение с параметром :
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства