Условие:
Из генеральной совокупности X , заданной таблицей, распределенной по нормальному закону, извлечена выборка
g = 0,99

Требуется:
Составить вариационный, статистический и выборочный ряды распределения; найти размах выборки;
По полученному распределению выборки:
- Построить полигон относительных частот;
- Вычислить выборочную среднюю, выборочную дисперсию, выборочное исправленное среднее квадратическое отклонение, моду и медиану;
- С надежностью g найти доверительные интервалы для оценки математического ожидания изучаемого признака генеральной совокупности.
Решение:
1) Введем обозначения:
xi зафиксированные значения признака
ni частоты
n=ni =40 - объем выборки
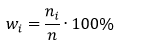
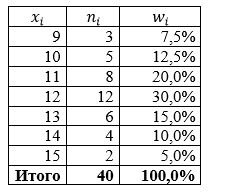
Получаем ряд распределения:
2) Изобразим полигон относительных частот:
