Условие задачи
Два друга купили лотерейные билеты, один – 10, другой – 15 штук. Каково наиболее вероятное число билетов, по которым может выиграть каждый из них, если вероятность выигрыша на один билет равна 1/4? Найти математическое ожидание и дисперсию случайного числа выигранных билетов, купленных первым из двух друзей.
Ответ
Наивероятнейшее число успехов в схеме Бернулли это целое число, заключенное в интервале
. Если одно из этих числе целое, то и другое целое, и невероятнейших чисел два: 
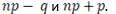
вероятность выигрыша на один...
Потяни
