Условие задачи
1. Выборка 2: 0,54; 0,42; 0,31; 0,61; 0,43; 0,35; 0,48; 0,55; 0,66; 0,50; 0,75; 0,40.
1). Требуется:
1а. Определить объем выборки.
1б. Найти оценку для среднего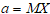 
.
1в. Найти оценку для дисперсии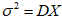 
.
1г. Найти оценку для вероятности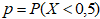 
.
2. Построить доверительный интервал
2а. – интервал для среднего а, имеющий точный уровень доверия 0,99.
2б. – для среднего а, имеющий точный уровень доверия 0,9.
2в. – для дисперсии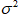 
, имеющий точный уровень доверия 0,99.
2г. – для дисперсии 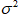, имеющий точный уровень доверия 0,9.
2д. – для вероятности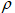 
, имеющий асимптотический уровень доверия 0,99.
2е. – для вероятности 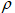, имеющий асимптотический уровень доверия 0,9.
3. Рассмотрим следующую гипотезу об истинном значении среднего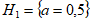 
.
6а. Построить критерий для проверки гипотезы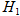 
имеющий точный критический уровень 0,01.
6б. Построить критерий для проверки гипотезы 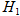имеющий точный критический уровень 0,1.
Ответ
1. Запишем данные в виде вариационного ряда, упорядочив значения по возрастанию:
1а. объем выборки (число вариант выборки) n = 12.
1б. оценку для среднего найдем по формуле средней арифметической:
