Условие задачи
Семья Ивановых раз в неделю ест грибной суп. Известно, что вероятность отравления равна 0,1.
Какова вероятность того, что за 5 недель они ни разу не попадут в больницу?
Предполагается, что Ивановы не изменят традиции даже после отравления и каждую неделю едят собранные накануне грибы.
Для ДСВ – количества отравлений построить ряд распределения и график функции распределения, найти математическое ожидание и дисперсию. Показать найденную вероятность на графике функции распределения.
Ответ
В задаче речь идет о повторных независимых испытаниях. Успехом будем считать отравление семьи Ивановых.
Для нахождения вероятности ровно k успехов в n испытаниях применим формулу Бернулли:
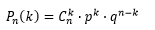
По условию:
Потяни
