Условие:
Случайная величина X ∈ N (1;2). Случайная величина Y связана с X функциональной зависимостью Y=3X–1. Найти g(y) – плотность вероятности случайной величины Y, EY, DY=σy2. С помощью таблиц приближенно вычислить P(|Y-EY|<1,0σy) и P({1≤Y<20}).
Решение:
Функция распределения нормальной распределенной величины:
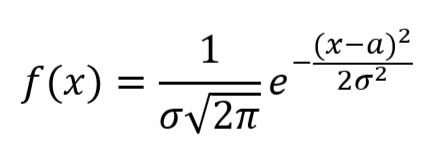
Для нашего распределения случайной величины Х:
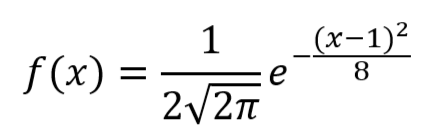
Плотность распределен...
