Условие:
1. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 8 и 1. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (10;12).
2. Найти выборочную дисперсию по данному распределению объёма выборки n=20:
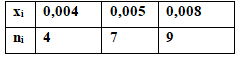
Решение:
1. Вероятность попадания в интервал нормально распределённой случайной величины найдём по формуле:
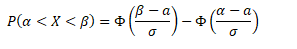
Тогда получаем, что искомая вероятность равна:
