Условие задачи
Среди кандидатов в студенческий совет факультета 3 первокурсника, 5 второкурсников и 7 третьекурсников. Из этого состава наудачу выбирают 5 человек. Найти вероятность следующих событий: A={будут выбраны одни третьекурсники}; B={все первокурсники попадут в эту группу}; C={не будет выбрано ни одного второкурсника}.
Ответ
а) Событие A будут выбраны одни третьекурсники.
Решим данную задачу, используя формулу классического определения вероятности, которая выглядит так:
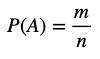
В данной формуле:
n- количество всех возможных элементарных исходов;
m- количество благоприятных событию A исходов.
Количество всех возможных исходов складывается из количества способов выбрать 5 студентов среди всех имеющихся студентов, поэтому данное кол...
Потяни
