В группе из двадцати пяти студентов имеется пять отличников. Выбираются наудачу три студента. Какова вероятность, что все они отличники, хотя бы один отличник.
«В группе из двадцати пяти студентов имеется пять отличников. Выбираются наудачу три студента. Какова вероятность, что все они отличники, хотя бы один отличник.»
- Теория вероятностей
Условие:
В группе из 25 студентов имеется 5 отличников. Выбираются наудачу три студента. Какова вероятность, что все они отличники, хотя бы один отличник.
Решение:
Найдем общее число исходов. Выбрать 3 студента означает составить группу из 3 студентов, если их всего 25, причем порядок выбора безразличен. Значит, речь идет о сочетаниях по 3 элементам из 25. Число таких сочетаний равно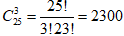 
.
А) Исход является благоприятным, если из случайно отобранных трех студентов все являются отличники. Согласно правилу произведения число благоприятных исходов равно .
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э