В новогодней лотерее 25 билетов, 10 из которых выигрывают. Гражданин купил 4 билета. Какова вероятность того, что 1) три будут выигрышными; 2) по крайней мере один из купленных билетов выигрышный?

1)Пусть событие A-три билета будут выигрышными из 4-х купленных билетов.

Решим данную задачу, используя формулу классического определения вероятности, которая выглядит так:

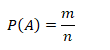
В данной формуле:

n- количество всех возможных элементарных исходов;

m- количество благоприятных событию A исходов.

Общее количество исходов равно количеству способов купить 4 билета из 25 билетов, данное количество способов найдём ...