Условие задачи
В партии, содержащей 20 деталей, имеются четыре с дефектами. Наудачу взяли для проверки три детали. Случайная величина Х – число дефектных деталей среди отобранных. Найти:
а) закон распределения этой случайной величины;
б) построить многоугольник распределения;
в) вычислить математическое ожидание;
г) определить дисперсию;
д) составить функцию распределения F(x) и построить ее график.
Ответ
а) Введем дискретную случайную величину Х = (число дефектных изделий среди проверяемых).
Х может принимать значения 0, 1, 2, 3 так как выбираются 3 изделия, а всего дефектных изделий 4, исправных 20-4=16.
Найдем соответствующие вероятности по формуле гипергеометрической вероятности
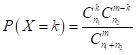
где n1 - количество дефектных изделий,
n2 - количество исправных изделий,
m - общее количество выбранных изделий.
