В первой урне 5 белых, 2 синих и 3 красных шаров, во второй урне 5 белых, 3 синих и 2 красных шаров, в третьей урне 3 белых, 2 синих и 5 красных шаров. Из каждой урны наудачу извлекают по одному шару.
«В первой урне 5 белых, 2 синих и 3 красных шаров, во второй урне 5 белых, 3 синих и 2 красных шаров, в третьей урне 3 белых, 2 синих и 5 красных шаров. Из каждой урны наудачу извлекают по одному шару.»
- Теория вероятностей
Условие:
В первой урне 5 белых, 2 синих и 3 красных шаров, во второй урне 5 белых, 3 синих и 2 красных шаров, в третьей урне 3 белых, 2 синих и 5 красных шаров. Из каждой урны наудачу извлекают по одному шару.
Какова вероятность того, что среди извлеченных шаров:
а) хотя бы один будет красный шар?
б) будет только один красный шар?
в) все извлеченные шары будут одного цвета?
Решение:
В первой урне: Б-5, С-2, К-3
Во второй урне: Б-5, С-3, К-2
В третьей урне: Б-3, С-2, К-5
Рассмотрим событие
а) А- из 3 урн извлечен хотя бы один красный шар
Рассмотрим противоположное событие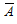 
- извлеченные шары не красные
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э