Условие:
Заданы плотности распределений равномерно распределенных независимых случайных величин X и Y:
f1(x) = 1/2 в интервале (1,3), вне этого интервала f1(x) = 0;
f2(y) = 1/4 в интервале (2,6), вне этого интервала f2(y) = 0.
Найти функцию распределения и плотность распределения случайной величины Z = X + Y. Построить график плотности распределения g(z).
Решение:
По условию, возможные значения X определяются неравенством 1 х 3, возможные значения Y - неравенством 2 у 6.
Отсюда следует, что возможные случайные точки (X; Y) расположены в прямоугольнике ОАВС .
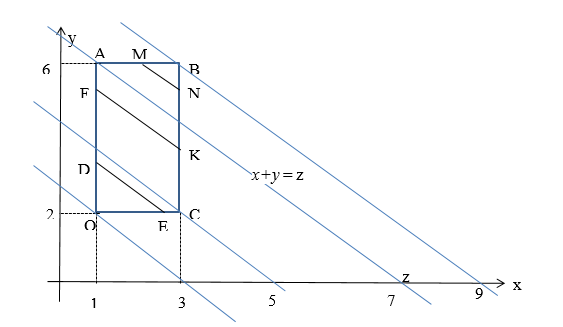
По определению функции распределения,
