Условие задачи
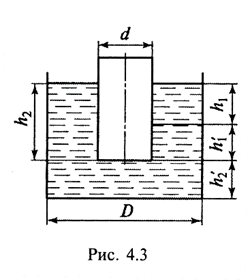
Свободная поверхность жидкости в резервуаре находится на расстоянии h1′ + h2′ от его основания. После погружения цилиндра диаметром d расстояние до свободной поверхности стало равным h1 + h1′ + h2′. Определить диаметр d цилиндра, если h1 = 200 мм, h2 = 288 мм, D = 60 мм (рис. 4.3).
Ответ
По закону Архимеда, в результате погружения цилиндра на глубину h1, вес вытесненной воды равен весу воды в объеме погруженного тела, а архимедова сила весу воды, вытесненной погружением цилиндра, т.е.
G = PA
Потяни
