Решение задачи
Доказать, что векторы образуют базис в . Найти координаты вектора в этом базисе и вектора в исходном, если в новом базисе:
- Высшая математика
Условие:
Доказать, что векторы 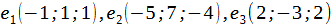 образуют базис в
образуют базис в 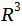 . Найти координаты вектора
. Найти координаты вектора 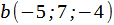 в этом базисе и вектора в исходном, если в новом базисе:
в этом базисе и вектора в исходном, если в новом базисе: 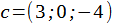
Решение:
Из координат векторов 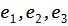 составим матрицу и найдем ее ранг:
составим матрицу и найдем ее ранг:
Вычислим определитель матрицы перехода:
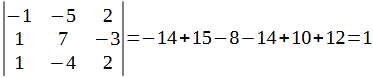
Так как определитель не равен нулю, то векторы линейно независимы и могут быть приняты в качестве базиса...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э