👋 Решение задач
📚 Высшая математика
решение задачи на тему:
Дата добавления: 13.07.2024
Двое игроков бросают по очереди монету. Выигравшим считается тот, кто первым откроет цифру. Во сколько раз более вероятным является выигрыш начавшего, если бросание может быть продолжено сколь угодно долго.
Ответ
Обозначим буквой А событие - выигрыш первого игрока, начавшего игру, В событие - выигрыш второго игрока.
При бросании монетки один раз вероятность выпадения цифры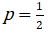 
, герба - 
.
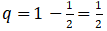событие - появление циф...
Сводка по ответу
Купи подписку Кампус+ и изучай ответы
Материалы со всех ВУЗов страны
1 000 000+ полезных материалов
Это примеры на которых можно разобраться
Учись на отлично с библиотекой
Набор самых полезных инструментов, работающих на искусственном интеллекте для студентов всего мира.
Экосистема
Кампус
Экосистема сервисов для учебы в удовольствие
Hit
Кампус AI
Твой второй пилот в учебе, быстрые ответы на основе AI
Hit
Кампус Эксперт
ТОП-эксперты помогут решить и объяснят тебе любой вопрос по учебе онлайн
NEW
Кампус Чатс
Сообщество, где ты найдешь знакомства и получишь помощь
Hit
Кампус Хаб
Мультифункциональный умный бот, который всегда под рукой
NEW
Библиотека
База знаний из 1 000 000+ материалов для учебы
