Используя метод Квайна, найти МДНФ для функции f (x1 , x2 ,x3), принимающей значение 1 на наборах: 2,3,4,5,7. Минимальная дизъюнктивная нормальная форма.

1. Составляется таблица 1 истинности, по которой и записываются все минтермы.

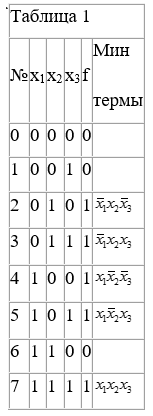
2. Составляется таблица 2.

Склеиваются импликанты последовательно: 1-2,1-3,1-4,1-5. Возможным оказалось склеивание импликат 1-2, около них поставим метку, получилась импликанта второго ранга, которая записывается во вторую колонку таблицы 2. Далее склеиваются 3-4,3-5. Склеивание 3-4 получает , около них поставим метку. Ост...