Условие:
Найти общее решение дифференциального уравнения:
y''+6y'+9y=x2 e-3x
Решение:
y''+6y'+9y=x2e-3x
Это неоднородное дифференциальное уравнение с постоянными коэффициентами. Найдем общее решение соответствующего однородного дифференциального уравнения:
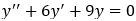
Составим характеристическое уравнение и найдем его корни:
