Пусть μ ∈ R, σ > 0 (оба неизвестны) и Х1,..., Хη ~ Ν(μ, σ²) - независимые случайные величины (n ≥ 2). Дана реализация этих величин х = (x1,..., xn) Rn (a) Вычислите статистику, необходимую для построения теста отношения правдоподобия для проверки гипотез
- Высшая математика
Условие:
Пусть μ ∈ R, σ > 0 (оба неизвестны) и Х1,..., Хη ~ Ν(μ, σ²) - независимые случайные величины (n ≥ 2). Дана реализация этих величин х = (x1,..., xn) Rn
(a) Вычислите статистику, необходимую для построения теста отношения правдоподобия для проверки гипотез
H0 : μ <= μ0 versus H1 : μ > μ0
(b) Покажите, что тест, основанный на этой статистике эквивалентен одностороннему - критерию Стьюдента для проверки этих же гипотез.
Решение:
a) В критерии отношения правдоподобия статистика имеет вид
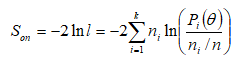
При верной гипотезе эта статистика асимптотически распределена так же, как и статистика Пирсона.
При практическом использовании критериев согласия выбирают либо интервалы равной длины, либо интервалы равной вероятности (равной частоты), либо асимптотически оптимальные интервалы (в этом случае минимизируются потери в информации Фишера) Разбие...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства