1. Главная
  2. Библиотека
  3. Высшая математика
  4. Разложить в ряд по степеням x функцию y=cos⁡5x. Проведем разложение по формуле f(x)=f(0)+f^' (0)x+x^2/2! f^'' (0)+⋯+x^n/n...

Разложить в ряд по степеням x функцию y=cos⁡5x. Проведем разложение по формуле f(x)=f(0)+f^' (0)x+x^2/2! f^'' (0)+⋯+x^n/n! f^((n) ) (0)+x^(n+1)/(n+1)! f^((n+1) ) (θx). Пусть 5x=z, тогда

«Разложить в ряд по степеням x функцию y=cos⁡5x. Проведем разложение по формуле f(x)=f(0)+f^' (0)x+x^2/2! f^'' (0)+⋯+x^n/n! f^((n) ) (0)+x^(n+1)/(n+1)! f^((n+1) ) (θx). Пусть 5x=z, тогда»
  • Высшая математика

Условие:

Разложить в ряд по степеням x функцию y = cos⁡ 5x.

Решение:

Проведем разложение по формуле:

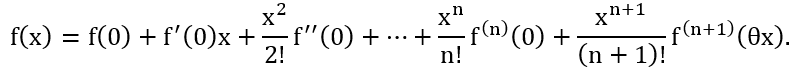
Пусть 5x = z, тогда

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я