Условие:
Решить волновое уравнение с ненулевыми граничными условиями методом разделения переменных Фурье
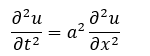
с граничными условиями u(0,t)=b;u(l,t)=c и начальными условиями u(x,0)=f(x), ∂u(x,0)/∂t=ϕ(x).

Решение:
Имеем следующую задачу:
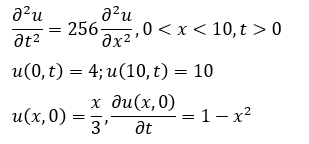
Решение задачи представим суммой функций
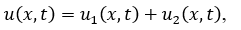
где функция
