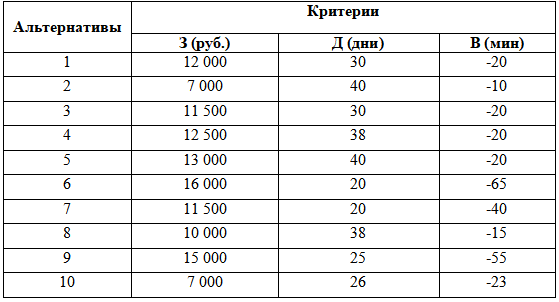
Требуется выбрать место работы из 10 альтернативных вариантов, представленных в Таблице. В качестве критериев выбраны: З- зарплата, Д- длительность отпуска, В- время поездки до работы.
- Высшая математика
Условие:
Требуется выбрать место работы из 10 альтернативных вариантов, представленных в Таблице. В качестве критериев выбраны: З- зарплата, Д- длительность отпуска, В- время поездки до работы. Так как последний критерий имеет характер потерь, то оценки по нему берутся со знаком « - ».
Выделить парето-оптимальное множество Mп.
Провести сужение множество Mп методами:
- указание нижних границ критериев;
- субоптимизации;
- лексикографической оптимизации;
- линейной свертки.
3.2. На вакантную должность D имеется 6 претендентов: a, b, c, d, e, f. Выбрать 8 критериев оценки P, Q, R, S, X, T, Y, Z. Для каждого критерия разработать несколько вариантов ответа, оценив их количественно от 1 до 9.
Требуется:
1. Словесно описать каждого из претендентов по каждому из критериев.
2. Сформировать векторные оценки претендентов.
3. Провести процедуру квантификации, оценив количественно каждый параметр. Сформировать множество векторов V = {a, b, c, d, e, f} с количественными оценками.
4. Оценить множество V по Парето. При этом оценки каждого вектора должны быть сформированы таким образом, чтобы в паретооптимальном множестве МП осталось 2-3 вектора.
5. Предложить метод сужения паретооптимального множества МП, по которому выбрать одного претендента на вакантную должность.
3.3. Решить задачу выбора методом анализа иерархий. Разработать 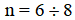 критериев и
критериев и 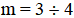 альтернативы.
альтернативы.
Графически изобразить иерархию задачи.
Упорядочить критерии по невозрастанию их важности. Подсчитать вклад каждого критерия в общую цель.
Выполнить попарные сравнения альтернатив относительно каждого критерия оптимальности.
Определить глобальные приоритеты альтернатив методом линейной свертки.
В качестве искомой выбрать альтернативу с максимальной оценкой.
3.4. В задаче из п. 3.3 для каждой альтернативы определить конкретные значения, представленные нечеткими множествами.
Решить задачу методом пересечения нечетких множеств.
3.5. Составить отчет по практической работе.
3.6. Ответить на контрольные вопросы.
Решение:
Векторная оценка d = (d1, d2, , dk) доминирует по Парето векторную оценку  если для любого j = 1, , k имеет место
если для любого j = 1, , k имеет место
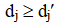 и, по крайней мере, для одного индекса j неравенство является строгим.
и, по крайней мере, для одного индекса j неравенство является строгим.
Исход a1 домин...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства