1. Главная
  2. Библиотека
  3. Высшая математика
  4. y^'-y/(x+1)=1 , y(0) = 1; [0;1], h=0,1 Найти точное решение задачи Коши для обыкновенного дифференциал...

y^'-y/(x+1)=1 , y(0) = 1; [0;1], h=0,1 Найти точное решение задачи Коши для обыкновенного дифференциального уравнения перового порядка. Используя метод Эйлера, составить таблицу приближенных значений решение дифференциального уравнения

«y^'-y/(x+1)=1 , y(0) = 1; [0;1], h=0,1 Найти точное решение задачи Коши для обыкновенного дифференциального уравнения перового порядка. Используя метод Эйлера, составить таблицу приближенных значений решение дифференциального уравнения»
  • Высшая математика

Условие:

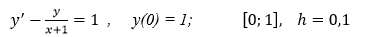
Найти точное решение задачи Коши для обыкновенного дифференциального уравнения перового порядка. Используя метод Эйлера, составить таблицу приближенных значений решение дифференциального уравнения на отрезке [0; 1] с шагом h = 0,1 и начальным условием y(0) = 1. Найти относительную погрешность полученного приближенного значения решения в точке x = 2, сопоставив его с точным решением.

Решение:

Данное уравнение является линейным. Его решение найдем методом произведения.

Пусть y = uv, тогда y' = u' v + uv'.

Подставив в уравнение получим

Пусть

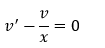
то есть

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я