Условие задачи
Задан граф состояний цепи Маркова с непрерывным временем. В начальный момент времени система находится в состоянии 𝑆1. Требуется:
1) составить матрицу интенсивностей переходов;
2) составить систему дифференциальных уравнений Колмогорова;
3) не решая самой системы, найти предельное стационарное распределение вероятностей;
4) получить численное решение системы уравнений Колмогорова с шагом ∆t=0,05 и убедиться, что при достаточно большом времени оно выходит на стационарное решение.
Ответ
1) Матрицу интенсивностей переходов строим по размеченному графу состояний: на главной диагонали стоит сумма всех исходящих потоков из соответствующей вершины, на остальных местах интенсивности ij переходов между состояниями i, j (например, интенсивности перехода из состояния S2 в S1 соответствует 21 = 2 ):
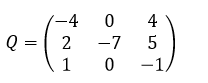
2) Систему дифференциальных уравнений Комогорова записываем по составленной матрице и...
