Условие:
Исследовать поведение линейной системы в виде фильтра нижних частот (ФНЧ) на входные сигналы разной формы.
Исходные данные: Задан ФНЧ в виде линейного звена второго прядка, описываемого дифференциальным уравнением
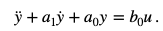
Коэффициенты уравнения (2.1) для заданного варианта представлены в табл.2.1.

Требуется:
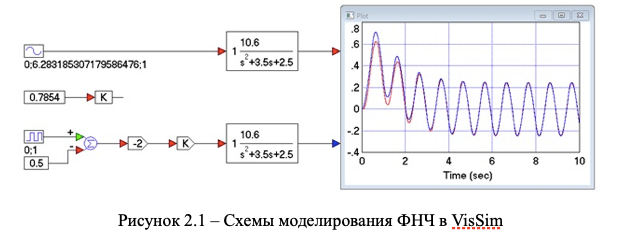
1) Составить и набрать две одинаковых схемы с плоттерами для моделирования на VisSim, соответствующих (2.1). Подать на вход первой схемы с весовым коэффициентом сигнал в виде прямоугольной волны, на вход второй схемы – синусоиду с единичной амплитудой. Сигналы можно подать так, показано на рисунке 1 Практики 8. Установить частоту сигнала в виде прямоугольной волны равной 1 с-1.
2) Определить (сделать вывод) такого значения весового коэффициента для сигнала в виде прямоугольной волны в первой схеме, чтобы амплитуда первой гармоники этой волны была равна амплитуде синусоиды во второй схеме. Подсчитать частоту синусоиды, чтобы ее период повторения был равен периоду повторения прямоугольной волны. Установить на схеме п.1 найденные и заданные коэффициенты. Схемы и подробные расчеты с пояснениями поместить в отчет по работе.
3) Выполнить моделирование по времени, то есть получить временные диаграммы для обеих схем. Длительность интегрирования выбрать 10 с. Сравнить выходные процессы. Результаты поместить в отчет.
4) Сделать выводы по работе.
Решение:
1. Схемы для моделирования в программе VisSim приведена на рис.2.1.
Передаточная функция ФНЧ, соответствующая ДУ (2.1)
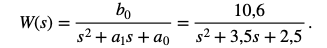
На вход верхней схемы подается синусоида единичной амплитуды. На вход нижней схемы ...
