Условие:
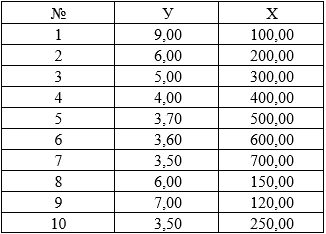
Изучается зависимость материалоёмкости продукции у (количество материалов на единицу продукции) от размера предприятия х (выпуск продукции, тыс. ед.) по 10 однородным заводам. Исходные данные приведены в таблице 1.
Таблица 1
Исходные данные
Требуется:
1. Постройте корреляционное поле и сформулируйте гипотезу о форме связи.
2. Оцените параметры уравнений линейной, степенной, обратной, экспоненциальной, логарифмической, парной регрессии.
3. Оцените тесноту связи при помощи коэффициента корреляции, индекса корреляции, коэффициента детерминации.
4. Используя средний (общий) коэффициент эластичности, дайте сравнительную оценку силы связи фактора с результатом.
5. Оцените при помощи средней ошибки аппроксимации качество уравнений.
6. С помощью t-критерия Стьюдента оцените статистическую надёжность оценок коэффициентов регрессии.
7. С помощью F-критерия Фишера-Снедекора оцените статистическую надёжность результатов регрессионного моделирования, выберите наилучшее уравнение регрессии по значениям характеристик, рассчитанных в пп. 4, 5.
8. Рассчитайте значение статистики DW (Дарбина-Уотсона) и сделайте вывод о наличии автокорреляции в ряду остатков.
9. Рассчитайте прогнозное значение результата, если значение фактора увеличится на 10 % от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости а = 0,05.
10. Полученные результаты и выводы оформите в аналитической записке.
Решение:
1. Корреляционное поле между материалоёмкостью продукции у (количество материалов на единицу продукции) и размером предприятия х (выпуск продукции, тыс. ед.) приведено на рисунке 1.
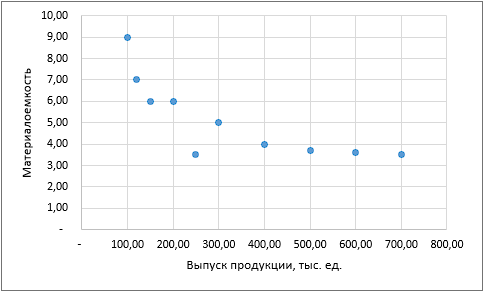
Рисунок 1 Корреляционное поле
На основании построенного корреляционного поля можно предположить о наличии обратной степенной связи вида: , но не исключено, что зависимость может качественнее описываться иной функцией.
