Однородная круглая платформа массой M и радиусом R может вращаться без трения вокруг неподвижной вертикальной оси O, перпендикулярной к её плоскости. По окружности платформы может двигаться материальная точка B массой m.

24 января 2025
Механика

Условие:

Однородная круглая платформа массой M и радиусом R может вращаться без трения вокруг неподвижной вертикальной оси O, перпендикулярной к её плоскости. По окружности платформы может двигаться материальная точка B массой m. В начальный момент система неподвижна, затем точка B начинает двигаться относительно платформы по закону s=R(1-cos⁡kt) [м], где k=const, t – время (положительное направление дуг – против часовой стрелки). Определить закон вращения платформы.

Дано: M, R, m, s=R(1-cos⁡kt), м, k=const.

Найти: φ=φ(t).

Решение:

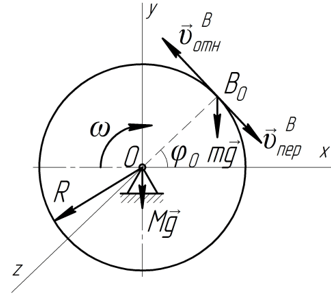
Рассмотрим механическую систему, состоящую из платформы и груза В. Для определения применим теорему об изменении кинетического момента системы относительно оси z:

(1)При движении точки в одну сторону, платформа будет вращаться в противоположном направлении.