1. Главная
  2. Библиотека
  3. Сопротивление материалов
  4. Раскрыть статическую неопределимость методом непосредственного интегрирования дифференциального уравнения изогнутой оси, о...

Раскрыть статическую неопределимость методом непосредственного интегрирования дифференциального уравнения изогнутой оси, определить реакции закрепления.

«Раскрыть статическую неопределимость методом непосредственного интегрирования дифференциального уравнения изогнутой оси, определить реакции закрепления.»
  • Сопротивление материалов

Условие:

Для статически неопределимой балки (см. рис. к задаче 4):

1. Раскрыть статическую неопределимость методом непосредственного интегрирования дифференциального уравнения изогнутой оси, определить реакции закрепления.

 2. Построить эпюры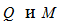 выразив все ординаты через интенсивность распределенной нагрузки  . 

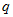3. Определить геометрические характеристики сложного сечения: положение центра тяжести и проходящей через него главной центральной оси инерции 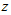 , осевой момент инерции  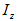 и осевой момент сопротивления  . 

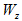4. Из условия прочности, приняв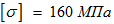 , определить грузоподъемность (значение  ). 

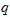5. Проверить условия жесткости и, если они не удовлетворяются, подобрать другое значение нагрузки  .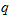

Исходные данные:

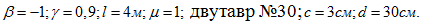
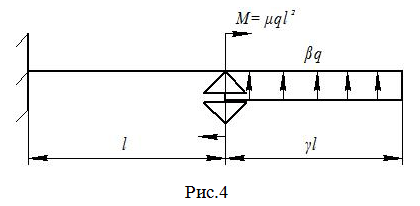
Решение:

1. Запишем уравнения равновесия для нее:

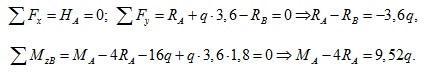
Как видно, неизвестных реакций здесь 4, а уравнений равновесия - только 3. Говорят, что степень статической неопределимости этой балки равна 1, или что балка один раз статически неопределима.

Как обычно, если для определения реакций не хватает уравнений статики, нужно записать уравнения совместности перемещений. Для балок в этом качестве используются условия ...

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я