Условие задачи
Два игрока показывают 1, 2 или 3 пальца. Если количество пальцев чётное, то выигрывает 1-й, если нечётное, то 2-й.
Банк может складываться разными способами:
1) каждый вкладывает по рублю до игры;
2) проигравший отдаёт противнику столько рублей, сколько пальцев в сумме они показали;
3) каждый платит столько, сколько пальцев он показал;
Составить игровые матрицы и проанализировать, кому из игроков выгоднее эта игра – первому или второму.
Ответ
В первом случае организации банка получаем игровую матрицу (для первого игрока)
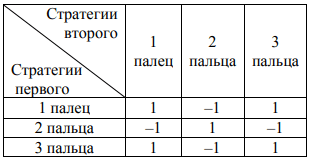
Бинарная матрица имеет вид
Потяни
