Условие:
По заданной плотности равномерного совместного распределения случайных величин Х и Y
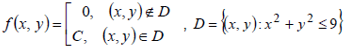
найти
1. параметр С;
2. плотности распределения компонент случайного вектора Х и Y;
3. функции распределения компонент случайного вектора Х и Y;
4. условные плотности 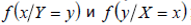 ;
;
5. выяснить, являются ли независимыми компоненты случайного вектора Х и Y;
6. числовые характеристики случайного вектора: математические ожидания и дисперсии случайных величин Х и Y, корреляционный момент и коэффициент корреляции, корреляционную матрицу и обобщенную дисперсию;
7. функции регрессии (условные математические ожидания) Y на Х и Х на Y, построить линии регрессии.
Решение:
1) Свойство плотности распределения
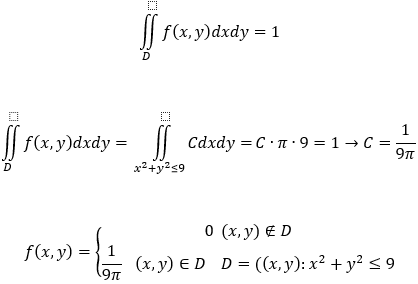
2)Плотность распределения X
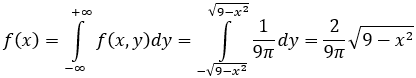
Плотность распределения Y
