Условие задачи
Сеть связи имеет структуру, изображенную на рис. 1 («мостик с двумя перемычками»). Рассматривается связь между двумя полюсами сети (выделены на рисунке заливкой). Предполагается, что связь возможна, если между полюсами сети существует работоспособный путь. Состояния всех линий независимы, узлы считаются абсолютно надёжными. Вероятности работоспособности линий pi (i = 1,…,6) для каждого варианта даны в табл. 3.
Рассчитать вероятность работоспособности (возможности связи между полюсами) сети, используя разложения по элементам (двум перемычкам).
Перечислить все простые пути и простые сечения системы.
Рассчитать нижнюю и верхнюю оценки вероятности работоспособности системы на основе попарно непересекающихся простых путей и сечений (оценки Литвака-Ушакова).
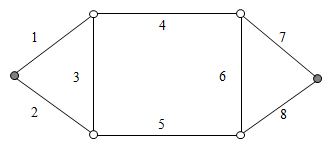
Рисунок 1. Схема сети связи («мостик с двумя перемычками»)
Таблица 3
Ответ
В качестве элементов разложения берём две перемычки элемент 3 и элемент 6. Обозначим через A событие работоспособности системы. Для его вероятности имеет место равенство:
P = P(A) = (1 p3)(1 p6) P{A | x3 = 0 и x6 = 0} +(1 p3)p6 P{A | x3 = 0 и x6 =1}+p3 (1 p6) P{A | x3 = 1 и x6 =0}+ p3p6 P{A | x3 = 1 и x6 =1}.
В каждой из рассмотренных ситуаций неработоспособность элемента разложения приводит к удалению соответствующего ребра из графа, а условие работоспособности элемента разложение к стягиванию (отождествлению) его граничных вершин.
При этом получаются системы, изображе...
