Условие:
Случайные величины X3 и X4 имеют равномерное и нормальное распределения соответственно. Найти вероятности P(1 < Xi < 2), если у этой случайной величины математическое ожидание и среднее квадратическое отклонение равны 1.
Решение:
1. Для равномерно распределенной на отрезке [a,b] случайной величины функция плотности имеет вид.
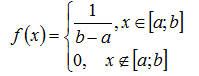
Математическое ожидание вычисляется по формуле:
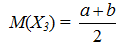
Дисперсия:
